Energía en el campo gravitatorio. Aplicaciones con satélites.

Este apartado de energía en el campo gravitatorio esta distribuido de la siguiente forma:

¿Qué es un campo de fuerzas conservativo?

Un campo de fuerzas es conservativo si el trabajo realizado por las fuerzas del campo no depende de la trayectoria que sigue el objeto para llegar de un punto A a un punto B. Si el campo es conservativo, entonces también lo es la fuerza.

$W_{A\rightarrow B}=W_{A\rightarrow B\rightarrow C}$

Ejemplos de fuerzas conservativas son la fuerza eléctrica y la fuerza gravitatoria.

Ejemplos de fuerzas no conservativas son la fuerza de rozamiento y la fuerza magnético.

Una fuerza conservativa, y por lo tanto un campo conservativo, lleva asociada una energía potencial.

El trabajo se define mediante la siguiente fórmula:

$W_{A\rightarrow B}=\int^B_A \vec F_g\cdot d\vec r$

La energía potencial es la función resultante de resolver esta integral.

$W_{A\rightarrow B}=\int^B_A \vec F_g\cdot d\vec r=E_p(r_A)-E_p(r_B)$

Concepto de energía potencial en el campo gravitatorio.

La energía potencial gravitatoria se define como la energía necesaria para trasladar una masa $m$ desde el infinito hasta un punto a una distancia $r$ de otra masa $M$ . El valor de la energía potencial en un punto se obtiene con la siguiente fórmula:

$E_p=-\dfrac{GMm}{r}$

La energía potencial es una magnitud escalar (un número, no un vector) y sus unidades en el sistema internacional son julios [J].

El trabajo necesario para trasladar una masa $m$ desde un punto A hasta un punto B es la menos variación de la energía potencial.

$W_{A\rightarrow B}=E_p(r_A)-E_p(r_B)=-\Delta E_p$

La energía potencial depende inversamente de la distancia entre las dos masas, por lo que a mayor distancia entre masas, menor energía potencial.

El análisis del signo del trabajo es muy útil para determinar si el resultado obtenido es válido. El signo del trabajo se analiza de la siguiente manera.

El signo del trabajo cuando se mueve una masa de un punto A a un punto B es positivo cuando la masa se aleja de la masa o las masas que generan el campo gravitatorio. Si por el contrario la masa se acerca el trabajo sería negativo.

Ejercicio de cálculo de la energía potencial.

Una masa puntual $m_A = 3 kg$ se encuentra en el plano xy, en el origen de coordenadas. Si se sitúa una masa puntual $m_B = 5 kg$ , en el punto P(2, -2) m, determine el trabajo necesario para llevar la masa B del punto P(2, -2) m al punto Q(2, 0) m debido al campo gravitatorio creado por la masa A.

Dato: Constante de gravitación universal $G=6'67\cdot10^{-11}Nm^2 kg^{-2}$ .

Solución

Para resolver este problema se tiene que calcular el trabajo mediante la energía potencial.

$W=-\Delta E_p\longrightarrow W=E_{pQ}-E_{pP}$

El primer paso es hallar las distancias entre el origen de coordenadas (punto en el que se encuentra la masa fija $m_A$ ) y los puntos P y Q (puntos inicial y final del movimiento de la masa que se mueve $m_B$ ).

$r_o=d(O,P)=\sqrt{2^2+(-2)^2}=2\sqrt{2}m$

$r_f=d(O,Q)=\sqrt{2^2+0^2}=2m$

Una vez que se tienen calculadas las distancias final e inicial se obtienen las energías potenciales.

$E_{pP}=-\dfrac{Gm_Am_B}{r_f}=-\dfrac{6'67\cdot10^{-11}Nm^2 kg^{-2}\cdot3kg\cdot5kg}{2\sqrt2m}=-3'53\cdot10^{-10}J$

$E_{pQ}=-\dfrac{Gm_Am_B}{r_f}=-\dfrac{6'67\cdot10^{-11}Nm^2 kg^{-2}\cdot3kg\cdot5kg}{2m}=-5\cdot10^{-10}J$

Tras esto se sustituye para obtener el valor del trabajo.

$W=-5\cdot10^{-10}J+3'53\cdot10^{-10}J=-1'47\cdot10^{-10}J$

Potencial gravitatorio.

El potencial se define como la energía por unidad de masa necesaria para trasladar un objeto desde un punto A a un punto B. El potencial gravitatorio es una magnitud escalar también y las unidades en las que se mide son los julios por kg [J/kg] y se calcula así:

$V_g=-\dfrac{GM}{r}$

Con el potencial se puede obtener también el trabajo mediante la siguiente relación:

$W_{A\rightarrow B}=-m\cdot \Delta V=-m(V_B-V_A)$

Ejercicio de cálculo de potencial.

El Sol tiene una masa de $1'989\cdot10^{30}kg$ . Calcule el potencial en la órbita de la Tierra y en la órbita de Marte.

Datos: constante de gravitación universal $G=6'67\cdot10^{-11} N\cdot m^2 \cdot kg^{-2}$ , distancia de la Tierra al Sol $r_{T-S}=1'5\cdot10^{11}m$ , distancia de Marte al Sol $r_{M-S}=2'25\cdot10^{11}m$ .

Solución

Para calcular el valor del potencial en la órbita de Marte utilizamos la siguiente ecuación:

$V_g=-\dfrac{GM_S}{r_{M-S}}=-\dfrac{6'67\cdot10^{-11} N\cdot m^2 \cdot kg^{-2}1'989\cdot10^{30}kg}{2'25\cdot10^{11}m}=-5'89\cdot10^{8}J/kg$

Para calcular el valor del potencial en la órbita de la Tierra utilizamos la siguiente ecuación:

$V_g=-\dfrac{GM_S}{r_{T-S}}=-\dfrac{6'67\cdot10^{-11} N\cdot m^2 \cdot kg^{-2}1'989\cdot10^{30}kg}{1'5\cdot10^{11}m}=-8'84\cdot10^8J/kg$

Principio de superposición para energía potencial y potencial.

Al igual que para el campo y para la fuerza, para la energía potencial y el potencial también se aplica el principio de superposición. La única diferencia con el campo y la fuerza es que la energía potencial y el potencial siempre son negativos, ya que, al no ser vectores, nunca se van a anular.

La energía potencial es la suma de las energías individuales.

$E_{pT}=E_{p1}+E_{p2}+E_{p3}...$

El potencial total en un punto es la suma cada uno de los potenciales generados por cada una de las masas en el mismo punto.

$V_{T}=V_{1}+V_{2}+V_{3}…$

Ejercicio de aplicación del principio de superposición.

Cuatro masas puntuales idénticas de 6kg cada una están situadas en los vértices de un cuadrado de lado 2m. Calcule el potencial gravitatorio creado por las cuatro masas en el centro del cuadrado.

Dato: constante de gravitación universal $G=6'67\cdot10^{-11}N\cdot m^2 \cdot kg^{-2}$ .

Solución

Lo primero que hay que hacer para resolver este problema es realizar un dibujo para orientar las masas en el espacio.

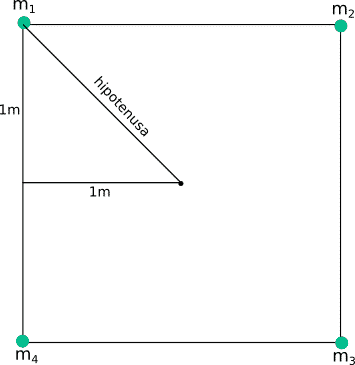
Tras esto hay que calcular las distancias de cada una de las masas al centro del cuadrado. Al ser un cuadrado la distancia del centro a las cuatro masas es la misma. Para hallar esta distancia podemos utilizar el teorema de pitágoras.

$r=\sqrt{1^2+1^2}=\sqrt2m$

Una vez que se han calculado las distancias utilizamos la ecuación del potencial para cada masa. Como en este caso las masas son iguales solo se necesita hallarlo una vez.

$V_g=V_{g1}=V_{g2}=V_{g3}=V_{g4}=-\dfrac{Gm}{r}=-\dfrac{6'67\cdot10^{-11}N\cdot m^2 \cdot kg^{-2}\cdot 6kg}{\sqrt2m}=$

$V_g=-2'83\cdot10^{-10}J/kg$

Después se aplica el principio de superposición para calcular el potencial total. Como los potenciales son iguales se multiplicaría el potencial por cuatro.

$V_{gT}=4\cdot V_g=4\cdot(-2'83\cdot10^{-10})J/kg=-1'13\cdot10^{-9}J/kg$

Conservación de la energía mecánica en el campo gravitatorio.

La energía mecánica es la suma de la energía cinética y las energías potenciales que existan, en el caso de la fuerza gravitatoria solo tendríamos energía potencial gravitatoria.

$E_m=E_c+E_p$

La fuerza gravitatoria es una fuerza conservativa. Partiendo de este concepto, podemos decir que la energía mecánica se conserva, es decir, que su variación es cero. Esto hace que los cálculos que se realizan en el movimiento de las órbitas se vuelvan mucho más sencillos.

$\Delta E_m=\Delta E_c+\Delta E_p=0$

Esta ecuación implica que $\Delta E_c=-\Delta E_p$ . Sabemos que la menos variación de energía potencial es el trabajo, por la definición de la energía potencial y que la variación de la energía cinética también lo es (teorema de las fuerzas vivas). Esto significa que el trabajo es igual al trabajo, por lo que acabamos de demostrar que se cumple la ecuación de conservación de la energía mecánica.

$\Delta E_c=W$

$-\Delta E_p=W$

$\Delta E_m=\Delta E_c+\Delta E_p=0\rightarrow\Delta E_c=-\Delta E_p\rightarrow W=W$

Movimiento de satélites con energía en el campo gravitatorio.

Con todo lo visto hasta ahora se pueden calcular múltiples magnitudes muy útiles en el movimiento de saltélites.

Velocidad de escape.

La velocidad de escape es la velocidad mínima que necesita un cuerpo para escapar de un campo generado por una masa M.

Partiendo de esta definición hay que utilizar la conservación de la energía mecánica para calcular la velocidad de escape.

$\Delta E_m=\Delta E_c+\Delta E_p=0$

$\Delta E_c=E_{cf}-E_{co}$

La energía cinética final es cero porque se pretende que la masa llegue solo hasta el punto en el que el campo deja de existir.

$E_{cf}=0$

La energía cinética inicial es la que existe al dotar a la masa de la velocidad que va a hacer que esta escape del campo gravitatorio.

$E_{co}=\dfrac{1}{2}mv_e^2$

$\Delta E_p=E_{pf}-E_{po}$

La energía potencial final es cero, ya que queremos que la masa escape del campo gravitatorio.

$E_{pf}=0$

La energía potencial inicial es la que tiene el cuerpo a la altura desde la que lo lanzamos para que escape del campo gravitatorio. Esta altura puede ser la superficie del planeta o una órbita. Para ambos casos vamos a llamar a esta distancia $r_o$ .

$E_{po}=-\dfrac{GMm}{r_o}$

Aplicando la conservación de la energía mecánica tenemos que:

$0-\dfrac{1}{2}mv_e^2+0+\dfrac{GMm}{r_o}=0$

Despejando la velocidad de escape obtenemos la siguiente fórmula:

$\dfrac{1}{2}mv_e^2=\dfrac{GMm}{r_o}$

$v_e=\sqrt{\dfrac{2GM}{r_o}}$

Lo más llamativo de esta solución es que la velocidad de escape no depende de la masa del cuerpo al que se quiera aplicar, sino de la masa del planeta en el que está (orbitando o en su superficie) y de la distancia al centro de este.

Por otro lado podemos relacionar la velocidad de escape con el módulo de la gravedad en el punto en el que se lanza el objeto. El módulo del campo en el punto en el que se lanza el cuerpo es:

$g_o=\dfrac{GM}{r_o^2}$

Si pasamos una $r_o$ al otro lado de la ecuación multiplicando obtenemos:

$g_or_o=\dfrac{GM}{r_o}$

Sustituyendo en la ecuación de la velocidad de escape tenemos:

$v_e=\sqrt{\dfrac{2GM}{r_o}}=\sqrt{2g_or_o}$

Ejercicio de cálculo de la velocidad de escape.

Calcule la velocidad de escape de un cuerpo de $m=200kg$ desde la superficie de la Tierra.

Datos: constante de gravitación unviersal $G=6'67\cdot10^{-11} Nm^2kg^{-2}$ ; radio de la Tierra $r_T=6371km$ ; masa de la Tierra $m_T=5'97\cdot10^{24}kg$ .

Solución

Para calcular la velocidad de escape se utiliza la ecuación:

$v_e=\sqrt{\dfrac{2GM_T}{r_T}}=\sqrt{\dfrac{2\cdot6'67\cdot10^{-11} Nm^2kg^{-2}\cdot5'97\cdot10^{24}kg}{6'371\cdot10^6m}}=11180'5m/s$

Velocidad orbital.

La velocidad orbital es la velocidad que tiene un cuerpo de masa $m$ al orbitar otro cuerpo de masa $M$ separados una distancia $r_o$ .

Analizando las fuerzas que intervienen en una órbita circular se puede concluir que existen dos: la fuerza centrífuga y la gravitatoria. Estas fuerzas tienen que tener el mismo módulo y dirección pero sentido contrario, ya que tienen que anularse para que el cuerpo tenga una velocidad angular constante al girar. La dirección de amabas fuerzas es la recta que une los centros de los dos cuerpos.

Para obtener la ecuación con la que poder calcular la velocidad orbital se empieza igualando los módulos de las fuerzas:

$F_g=F_c$

$\dfrac{GMm}{r_o^2}=m\dfrac{v_o^2}{r_o}$

$\dfrac{GM}{r_o}=v_o^2$

$v_o=\sqrt{\dfrac{GM}{r_o}}$

Al igual que con la velocidad de escape la velocidad orbital no depende de la masa del cuerpo que orbita, solo depende de la masa del cuerpo central y de la distancia entre los centros de ambos cuerpos.

También se puede relacionar la velocidad orbital con el módulo del campo gravitatorio en la órbita que describe el cuerpo.

$v_o=\sqrt{g_or_o}$

Ejercicio de cálculo de la velocidad orbital.

Calcule la velocidad orbital de la Tierra en su movimiento de traslación al rededor del Sol.

Datos: constante de gravitación unviersal $G=6'67\cdot10^{-11} Nm^2kg^{-2}$ ; masa del Sol $M_S=2\cdot10^{30}kg$ ; distancia de la Tierra al Sol $d_{T-S}=1'5\cdot10^{11}m$ .

Solución

Para calcular la velocidad orbital de la Tierra al rededor del Sol se utiliza la ecuación de la velocidad orbital.

$v_o=\sqrt{\dfrac{GM_S}{r_{S-T}}}=\sqrt{\dfrac{6'67\cdot10^{-11} Nm^2kg^{-2}\cdot2\cdot10^{30}kg}{1'5\cdot10^{11}m}}=29821'69m/s$

Energía orbital en el campo gravitatorio.

Una vez que sabemos como obtener la velocidad orbital, ya podemos calcular la energía orbital de un satélite, ya que esta sería la suma de la energía potencial y la energía cinética.

$E_o=E_m=E_p+E_c$

$E_o=-\dfrac{GMm}{r_o}+\dfrac{1}{2}mv_o^2$

Al introducir la fórmula de la velocidad orbital la energía orbital queda:

$E_o=-\dfrac{GMm}{r_o}+\dfrac{1}{2}m\dfrac{GM}{r_o}$

Si se opera la expresión queda que la energía orbital es:

$E_o=-\dfrac{1}{2}\dfrac{GMm}{r_o}=\dfrac{1}{2}E_p$

Energía de puesta en órbita en el campo gravitatorio.

Cuando se trata de poner un satélite en órbita se puede dividir el movimiento en dos partes para simplificarlo.

El primer movimiento sería el ascenso hasta la altura deseada y el segundo dotarle de la velocidad orbital correspondiente.

Vamos a analizar el primer movimiento.

Primero aplicamos la conservación de la energía mecánica en el primer movimiento.

$\Delta E_m=\Delta E_c+\Delta E_p=0$

$\Delta E_c=E_{cf}-E_{co}$

La energía cinética final es cero porque se pretende que la masa llegue solo hasta la altura a la que queremos colocar el satélite.

$E_{cf}=0$

La energía cinética inicial es la que existe al dotar a la masa de la velocidad ( $v_p$ ) que va a hacer que esta llegue hasta la altura que queremos.

$E_{co}=\dfrac{1}{2}mv_p^2$

$\Delta E_c=0-\dfrac{1}{2}mv_p^2$

$\Delta E_p=E_{pf}-E_{po}$

La energía potencial final es la producida por el planeta al estar a la altura a la que queremos situar el satélite ( $r_o=r_p+h$ es la distancia existente entre la órbita y el centro del planeta que se orbita).

$E_{pf}=-\dfrac{GMm}{r_o}$

La energía potencial inicial es la que tiene el cuerpo en la superficie del planeta ( $r_p$ es el radio del planeta).

$E_{po}=-\dfrac{GMm}{r_p}$

$\Delta E_p=-\dfrac{GMm}{r_o}+\dfrac{GMm}{r_p}$

Aplicando la conservación de la energía mecánica podemos obtener la velocidad necesaria para situar el satélite en una órbita circular a una distancia $r_o$ del centro del planeta:

$0-\dfrac{1}{2}mv_p^2-\dfrac{GMm}{r_o}+\dfrac{GMm}{r_p}=0$

$\dfrac{1}{2}mv_p^2=-\dfrac{GMm}{r_o}+\dfrac{GMm}{r_p}$

$v_p^2=2\left(-\dfrac{GM}{r_o}+\dfrac{GM}{r_p}\right)$

$v_p=\sqrt{2GM\left(\dfrac{1}{r_p}-\dfrac{1}{r_o}\right)}$

Una vez terminado con el primer movimiento, vamos a tratar el segundo movimiento.

En el segundo movimiento, la energía mecánica no se conserva, dado que las energías potenciales si son iguales, pero las cinéticas no. La energía necesaria para este movimiento sería la energía cinética producida por darle al satélite la velocidad orbital. Esta velocidad se aplica en el eje y.

$E_c=\dfrac{1}{2}mv_o^2$

Ejercicio de cálculo de la energía de puesta en órbita.

Se quiere poner en órbita un satélite de masa $m=200kg$ a una altura sobre la superficie de la Tierra del doble del radio de la Tierra. Calcule las velocidades que intervienen en la puesta en órbita y la energía cinética que hay que aportar al satélite una vez que estás a la altura deseada.

Datos: constante de gravitación unviersal $G=6'67\cdot10^{-11} Nm^2kg^{-2}$ ; radio de la Tierra $r_T=6371km$ ; masa de la Tierra $M_T=5'97\cdot10^{24}kg$ .

Solución

Primero se tiene que calcular la velocidad de puesta en órbita $v_p$ con su fórmula.

$v_p=\sqrt{2GM_T\left(\dfrac{1}{r_T}-\dfrac{1}{2r_T}\right)}$

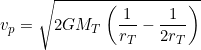
En un examen se recomienda demostrar la fórmula siguiendo los pasos de arriba ya que es más sencillo aprender la conservación de la energía que cada fórmula para cada caso.

$v_p=\sqrt{2\cdot6'67\cdot10^{-11} Nm^2kg^{-2}\cdot5'97\cdot10^{24}kg\left(\dfrac{1}{6'371\cdot10^6m}-\dfrac{1}{1'274\cdot10^7m}\right)}$

$v_p=7905'19m/s$

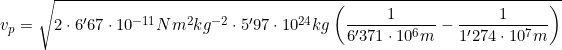
Tras esto se calcula la velocidad orbital.

$v_o=\sqrt{\dfrac{GM_T}{r_o}}=\sqrt{\dfrac{6'67\cdot10^{-11} Nm^2kg^{-2}\cdot5'97\cdot10^{24}kg}{1'274\cdot10^7m}}=5590'69m/s$

Una vez calculada la velocidad orbital se puede hallar la energía cinética.

$E_c=\dfrac{1}{2}m_sv_o^2=\dfrac{1}{2}200kg\cdot(5590'69m/s)^2=5'59\cdot10^5J$

Energía de cambio de órbita en el campo gravitatorio.

Un cambio de órbita consiste en aportar al satélite la suficiente energía cinética como para cambiar de órbita. Esto se consigue acelerando o decelerando el satélite hasta que la velocidad sea la velocidad orbital de la órbita nueva.

La energía cinética que habría que aportar al satélite sería la variación de las energías orbitales.

$\Delta E_c=E_{o2}-E_{o1}$

$\Delta E=-\dfrac{GMm}{2r_{o2}}+\dfrac{GMm}{2r_{o1}}$

Operando obtenemos:

$\Delta E=\dfrac{GMm}{2}\left(\dfrac{1}{r_{o1}}-\dfrac{1}{r_{o2}}\right)$

Ejercicio de cálculo de la energía de cambio de órbita.

Un satélite de $m=1200kg$ está orbitando a una altura de dos veces el radio de la Tierra y queremos cambiar su órbita para que su altura se duplique. Calcule la energía que se le tendrá que aportar al satélite.

Datos: constante de gravitación unviersal $G=6'67\cdot10^{-11} Nm^2kg^{-2}$ ; radio de la Tierra $r_T=6371km$ ; masa de la Tierra $M_T=5'97\cdot10^{24}kg$ .

Solución

La energía necesaria se obtendría con la ecuación:

$\Delta E=\dfrac{GM_Tm_s}{2}\left(\dfrac{1}{2r_T}-\dfrac{1}{4r_T}\right)$

En un examen se recomienda demostrar la fórmula siguiendo los pasos de arriba ya que es más sencillo aprender la conservación de la energía que cada fórmula para cada caso.

$\Delta E=\dfrac{6'67\cdot10^{-11} Nm^2kg^{-2}\cdot5'97\cdot10^{24}kg\cdot1200kg}{2}\left(\dfrac{1}{1'27\cdot10^7m}-\dfrac{1}{2'55\cdot10^7m}\right)$

$\Delta E=9'44\cdot10^9J$

Tipos de órbitas.

Tipos de órbitas según su energía.

Las órbitas de los satélites se pueden clasificar según su forma y energía.

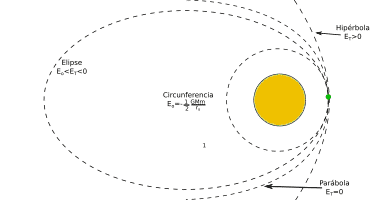
Circunferencia: en este tipo de órbita la distancia entre los centros de las dos masas es igual durante toda la oscilación. Esta órbita se produce cuando la energía total del satélite es negativa e igual a la mitad de la energía potencial en esta órbita.

$E_T=E_o=-\dfrac{GMm}{2r_o}<0$

Elipse: en este tipo de órbita el satélite describe una circunferencia «achatada». En esta órbita el planeta al que se orbita se sitúa en uno de los focos de la elipse. Esta órbita se da cuando la energía es negativa y su valor está entre la energía orbital de la circunferencia y cero.

$E_o<E_T<0$

Parábola: es una órbita abierta, por lo que este tipo de órbitas no genera satélites estables, es decir, el cuerpo gira y escapa de la acción del campo gravitatorio. Esta órbita se da cuando la energía es cero.

$E_T=0$

Hipérbola: es también una órbita abierta, pero mucho más abierta que la parábola. Esta órbita se da cuando la energía es positiva.

$E_T>0$

Otros tipos de órbitas.

Según la órbita y el periodo de los satélites se pueden clasificar los siguientes tipos:

Órbita geoestacionaria: este tipo de órbitas tienen su periodo alrededor de la Tierra es de 24h, por lo que siempre están sobre el mismo punto de la superficie.
Órbita geosíncrona: este tipo de órbitas son geoestacionarias y además su órbita está situada en el plano ecuatorial.

$\text{ }$