Inecuaciones con dos incógnitas. Apuntes.

Bienvenido al estudio de las inecuaciones con dos incógnitas. Aquí vamos a desarrollar un método para resolver este tipo de inecuaciones y ver como se aplica en unos cuantos ejemplos resueltos.

Más sobre inecuaciones

Inecuaciones de primer grado.

Resolución de inecuaciones de grado mayor que uno.

Inecuaciones racionales.

Sistemas de inecuaciones con una incógnita.

Una inecuación lineal con dos incógnitas es una expresión matemática que se puede escribir de la siguiente forma:

$ax+by+c\geq0$

$ax+by+c>0$

$ax+by+c<0$

$ax+by+c\leq0$

Este tipo de expresiones representa una región del plano XOY, es decir, son algo de este tipo:

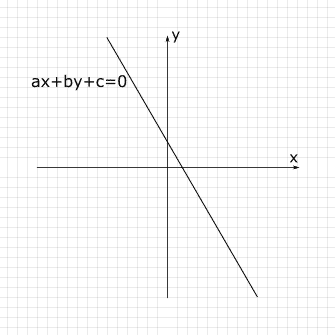
Recta ax+by+c=0. Método de resolución de inecuaciones con dos incógnitas

Si sustituimos en la inecuación los símbolos <, >, $\geq$ o $\leq$ (desigualdades) por un = (igual) obtendremos entonces la expresión de una recta en el plano, es decir, una expresión del tipo $ax+by+c=0$ .

Una vez que sabemos todo esto podemos empezar a explicar el método que vamos a utilizar para resolver este tipo de inecuaciones.

Método de resolución de inecuaciones con dos incógnitas.

Para resolver este tipo de inecuaciones hay que seguir los siguientes pasos:

1. Sustituimos en la inecuación la desigualdad (<, >, $\geq$ o $\leq$ ) por un igual (=). De esta forma obtendremos la ecuación de una recta.

$ax+by+c>0\longrightarrow{ax+by+c=0}$

2. Despejamos una de las dos incógnitas. Yo recomiendo despejar siempre la que veamos más sencilla (la que esté «sola»).

$x=\dfrac{-by-c}{a}$

$y=\dfrac{-ax-c}{b}$

3. Hacemos una tabla de valores. Para rellenarla se dan valores a la incógnita que no hemos despejado.

x	y
	0
	1

Si en el paso 2 has despejado la x se dan valores a la y. Para obtener los valores de x se sustituyen en la expresión del paso 2.

x	y
0
1

Si en el paso 2 has despejado la y se dan valores a la x. Para obtener los valores de y se sustituyen en la expresión del paso 2.

4. Dibujamos la recta uniendo los puntos obtenidos en el paso anterior.

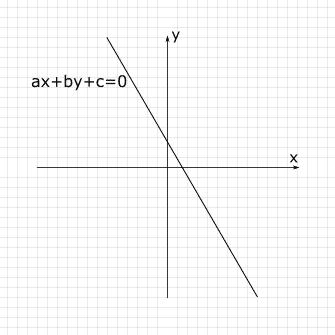
5. Una vez dibujada la recta, se busca cuál de las dos regiones en las que se divide el plano cuándo dibujamos la recta. Para lograr esto cogemos cualquier punto que cumpla la condición de no estar en la recta. Sustituimos el punto por las incógnitas en la inecuación del principio y vemos si cumple la inecuación. Si cumple la inecuación rallamos la parte dónde está ese punto, mientras que si no lo cumple rallamos la contraria.

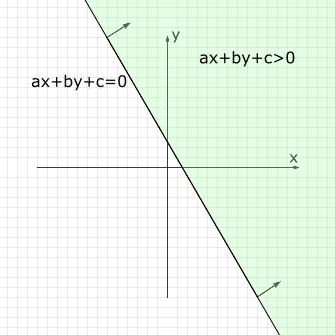
Recta ax+by+c=0 y semiplano ax+by+c>0. Método de resolución de inecuaciones con dos incógnitas

Es importante tener en cuenta que si la inecuación tiene los símbolos mayor y menor la recta se dibujará en discontinua, mientras que si tiene los símbolos mayor o igual y menor o igual se dibujará continua.

Ejemplo:

$2x-4y\leq6$

Para resolver esta inecuación seguimos los pasos que hemos visto arriba.

Primero convertimos la inecuación en ecuación sustituyendo la desigualdad por un igual.

$2x-4y\leq6\longrightarrow2x-4y=6$

Tras esto despejamos una de las incógnitas. en este caso es indiferente despejar cualquiera de las dos, así que voy a despejar la x.

$2x=6+4y\longrightarrow{x}=\dfrac{6+4y}{2}=3+2y$

Después hacemos la tabla dando valores aleatorios a la y para obtener los puntos que vamos a utilizar para representar la recta.

x	y
3	0
9	3

$x=3+2\cdot0=3$

$x=3+2\cdot3=9$

Ahora que hemos obtenido los puntos los dibujamos en la gráfica para unirlos y formar la recta.

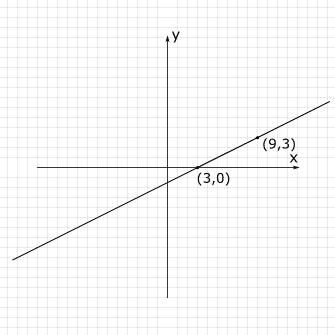
Tras esto, vamos a averiguar cual de los dos semiplanos en los que se divide ahora el plano es el que corresponde a la inecuación. Para hacer esto cogemos un punto cualquiera que esté fuera de la recta. Yo voy a coger el (0, 0). Después lo introducimos en la inecuación para ver si cumple.

$2x-4y\leq6\longrightarrow2\cdot0-4\cdot0\leq^?6$