Cálculo de determinantes de segundo y tercer orden.

Después de conocer las matrices, nos introducimos en el maravilloso mundo de los determinantes. Dentro de este mundo podremos ver cómo se estudia el rango de una matriz o cómo obtener la matriz inversa mediante métodos en los que utilizamos determinantes.

¿Qué es un determinante?

Un determinante es el valor numérico que se asocia a una matriz cuadrada. Dos matrices distintas pueden tener el mismo determinante y solo existen determinantes de matrices cuadradas. Una matriz se representa con paréntesis pero un determinante se representa entre barras y tiene un valor numérico.

Cómo calcular determinantes de orden 2.

Para calcular un determinante de segundo orden lo único que tenemos que hacer es restar los elementos de la diagonal principal multiplicados con los de la diagonal secundaría multiplicados, es decir:

$\left| \begin{matrix} a&b\\c&d\end{matrix} \right|=a\cdot d-b\cdot c$

Ejemplo

Obtenga el valor de los siguientes determinantes:

$\left| \begin{matrix} 1&2\\2&-1\end{matrix} \right|=1\cdot(-1)-2\cdot 2=-5$

$\left|\begin{matrix}0&3\\1&1\end{matrix}\right|=0\cdot1-3\cdot1=-3$

Cómo calcular determinantes de orden 3.

Para calcular determinantes de tercer orden aplicamos el método de Sarrus. Este método se puede aplicar de dos formas:

Primera forma:

Vamos a hacer el siguiente determinante:

$\left|\begin{matrix}a&b&c\\d&e&f\\g&h&i\end{matrix}\right|$

Para utilizar esta forma de aplicar el método de Sarrus tenemos que hacer la siguiente operación.

$=\left|\begin{matrix}a&&\\&e&\\&&i\end{matrix}\right|+\left|\begin{matrix}&&c\\d&&\\&h&\end{matrix}\right|+\left|\begin{matrix}&b&\\&&f\\g&&\end{matrix}\right|-\left|\begin{matrix}&&c\\&e&\\g&&\end{matrix}\right|-\left|\begin{matrix}&b&\\d&&\\&&i\end{matrix}\right|-\left|\begin{matrix}a&&\\&&f\\&h&\end{matrix}\right|=$

$=a\cdot e\cdot i+c\cdot d\cdot h+b\cdot f \cdot g-c \cdot e \cdot g-b\cdot d\cdot i-a \cdot f \cdot h$

Ejemplo

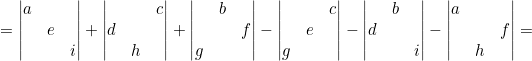
Obtén el valor del siguiente determinante:

$\left|A\right|=\left|\begin{matrix} 1&2&3\\4&5&6\\7&8&9\end{matrix}\right|$

$\left|A\right|=1\cdot 5\cdot 9+3\cdot 4\cdot 8+2\cdot 6\cdot 7-3\cdot 5\cdot 7-2\cdot 4\cdot 9-1\cdot 6\cdot 8=$

$=45+96+84-105-72-48=0$

Segunda forma:

Vamos a hacer el mismo determinante pero con la segunda forma:

$\left|A\right|=\left|\begin{matrix}a&b&c\\d&e&f\\g&h&i\end{matrix}\right|$

Lo primero sería añadir las dos primeras filas debajo del determinante.

$\left|A\right|=\left|\begin{matrix} a&b&c\\d&e&f\\g&h&i\\a&b&c\\d&e&f\end{matrix}\right|$

Multiplicamos los elementos de las diagonales paralelas a la diagonal principal.

$\begin{matrix} \\ \\ \end{matrix}\left|\begin{matrix} \boldsymbol{a}&b&c\\d&\boldsymbol{e}&f\\g&h&\boldsymbol{i}\\a&b&c\\d&e&f\end{matrix}\right| \begin{matrix} \\ \\ a \cdot e\cdot i \\ \\ \end{matrix}$

$\begin{matrix} \\ \\ \end{matrix} \left|\begin{matrix} a&b&c\\ \boldsymbol{d}&e&f\\g &\boldsymbol{h}&i\\a&b &\boldsymbol{c}\\ d&e&f\end{matrix}\right| \begin{matrix} \\ \\ a \cdot e\cdot i \\ d\cdot h \cdot c\\ \end{matrix}$

$\begin{matrix}\\ \\ \end{matrix}\left|\begin{matrix}a&b&c\\d&e&f\\\boldsymbol{g}&h&i\\a&\boldsymbol{b}&c\\d&e&\boldsymbol{f}\end{matrix}\right| \begin{matrix} \\ \\ a \cdot e\cdot i \\ d\cdot h \cdot c\\g\cdot b\cdot f\end{matrix}$

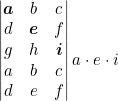
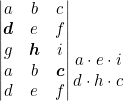
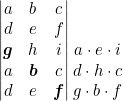
Sumamos los resultados.

$a\cdot e\cdot i+d\cdot h\cdot c+g\cdot b\cdot f$

Tras esto hacemos lo mismo con las paralelas a la diagonal secundaria.

$\begin{matrix} \\ \\ c\cdot e\cdot g\\ \\ \end{matrix} \left| \begin{matrix}a&b&\boldsymbol{c}\\d&\boldsymbol{e}&f\\\boldsymbol{g}&h&i\\a&b&c\\d&e&f\end{matrix}\right| \begin{matrix} \\ \\ \\ \\ \end{matrix}$

$\begin{matrix} \\\\c\cdot e\cdot g \\ f\cdot h\cdot a\\ \end{matrix} \left| \begin{matrix} a&b&c\\d&e&\boldsymbol{f}\\g&\boldsymbol{h}&i\\\boldsymbol{a}&b&c\\d&e&f\end{matrix}\right| \begin{matrix} \\ \\ \\ \\ \end{matrix}$

$\begin{matrix}\\\\c\cdot e\cdot g\\ f\cdot h\cdot a \\ i\cdot b \cdot d\end{matrix}\left|\begin{matrix} a&b&c\\d&e&f\\g&h&\boldsymbol{i}\\a&\boldsymbol{b}&c\\\boldsymbol{d}&e&f\end{matrix}\right| \begin{matrix} \\ \\ \\ \\ \end{matrix}$

$c\cdot e\cdot g+f\cdot h\cdot a+i\cdot b\cdot d$

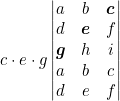
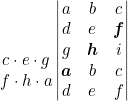
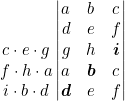
Restamos el resultado de las paralelas a la diagonal principal con los de la secundaria.

$a\cdot e\cdot i+d\cdot h\cdot c+g\cdot b\cdot f-(c\cdot e\cdot g+f\cdot h\cdot a+i\cdot b\cdot d)$

Ejemplo

Obtén el valor del siguiente determinante:

$\left|\begin{matrix}1&2&3\\4&5&6\\7&8&9\end{matrix}\right|$

$\begin{matrix}\\ \\ 105= 3\cdot 5\cdot 7 \\ 48=6\cdot 8 \cdot 1 \\ 72 = 9 \cdot 2 \cdot 4 \end{matrix} \left| \begin{matrix} 1&2&3 \\4&5&6 \\7&8&9 \\ 1&2&3 \\4&5&6 \end{matrix} \right| \begin{matrix} \\ \\ 1\cdot 5\cdot 9 = 45 \\ 4\cdot 8 \cdot 3 =96 \\ 7\cdot 2 \cdot 6 = 84 \end{matrix}$