Matriz adjunta y adjunto de un elemento.

Tras ver como calcular un determinante de orden dos y tres vamos a explicar que es el adjunto de un elemento y como calcular la matriz adjunta.

En los próximos temas vamos a ver la importancia de la matriz adjunta, y los adjuntos, dado que vamos a utilizarlos para calcular los determinantes de cualquier orden y la matriz inversa.

Ecuaciones matriciales

Determinantes de orden 2 y 3

Cálculo de determinantes de cualquier orden

Propiedades de los determinantes

Matriz inversa por determinantes

Rango de matrices con determinantes

Adjunto de un elemento.

El adjunto del elemento de la fila i, columna j sería el determinante de la matriz que quedaría al eliminar la fila i y columna j, multiplicado por $(-1)^{i+j}$ y se simboliza por: $A_{ij}$ .

Caso matriz de 2×2.

Para la matriz:

$A=\begin{pmatrix}a&b\\c&d\end{pmatrix}$

El adjunto del elemento de la primera fila primera columna sería:

$A_{11}=(-1)^{1+1}\cdot d=d$

Los demás serían:

$A_{12}=(-1)^{1+2}\cdot c=-c$

$A_{21}=(-1)^{2+1}\cdot b=-b$

$A_{22}=(-1)^{2+2}\cdot a=a$

Ejemplo

Hallar los adjuntos de todos los elementos de esta matriz:

$A=\begin{pmatrix}2&-1\\1&1\end{pmatrix}$

$A_{11}=(-1)^{1+1}\cdot 1=1$

$A_{21}=(-1)^{2+1}\cdot (-1)=1$

$A_{12}=(-1)^{1+2}\cdot 1=-1$

$A_{22}=(-1)^{2+2}\cdot 2=2$

Caso matriz de 3×3.

Supongamos que tenemos la matriz:

$A=\begin{pmatrix} a&b&c\\d&e&f\\g&h&i\end{pmatrix}$

En el caso del elemento de la segunda fila, primera columna sería:

$A_{21}=(-1)^{2+1}\left|\begin{matrix}b&c\\h&i\end{matrix}\right|=-1\cdot(b\cdot i-c\cdot h)$

El adjunto de la tercera fila segunda columna sería:

$A_{32}=(-1)^{3+2}\left|\begin{matrix}a&c\\d&f\end{matrix}\right|=-1\cdot(a\cdot f-c\cdot f)$

Ejemplo

Dada la matriz A, obtener los adjuntos de los siguientes elementos:

$A=\begin{pmatrix}3&-1&1\\2&1&0\\0&0&-2\end{pmatrix}$

a) Primera fila primera columna:

$A_{11}=(-1)^{1+1}\left|\begin{matrix}1&0\\0&-2\end{matrix}\right|=-2$

b) Segunda fila segunda columna:

$A_{22}=(-1)^{2+2}\left|\begin{matrix}3&1\\0&-2\end{matrix}\right|=-6$

c) Tercera fila segunda columna:

$A_{32}=(-1)^{3+2}\left|\begin{matrix}3&1\\2&0\end{matrix}\right|=2$

Matriz adjunta.

La matriz adjunta es se simboliza como $adj(A)$ y es la matriz que se genera sustituyendo los elementos de esta por sus adjuntos. Vamos es esto:

$adj(A)=\begin{pmatrix}A_{11}&A_{12}&A_{13}&\cdots&A_{1n}\\A_{21}&A_{22}&A_{23}&\cdots&A_{2n}\\A_{31}&A_{32}&A_{33}&\cdots&A_{3n}\\\vdots&\vdots&\vdots&\ddots&\vdots\\A_{n1}&A_{n2}&A_{n3}&\cdots&A_{nn}\end{pmatrix}$

Caso matriz 2×2.

Para una matriz de 2×2 como esta:

$A=\begin{pmatrix}a&b\\c&d\end{pmatrix}$

La matriz adjunta es:

$adj(A)=\begin{pmatrix}d&-c\\-b&a\end{pmatrix}$

Ejemplo

Obtener la adjunta de:

$A=\begin{pmatrix}4&3\\-1&-2\end{pmatrix}$

$adj(A)=\begin{pmatrix}-2&1\\-3&4\end{pmatrix}$

Caso matriz 3×3.

Cuando tenemos una matriz de 3×3 como:

$A=\begin{pmatrix}a&b&c\\d&e&f\\g&h&i\end{pmatrix}$

Su matriz adjunta sería:

$adj(A)=\begin{pmatrix}\left|\begin{matrix}e&f\\h&i\end{matrix}\right|&-\left|\begin{matrix}d&f\\g&i\end{matrix}\right|&\left|\begin{matrix}d&e\\g&h\end{matrix}\right|\\-\left|\begin{matrix}b&c\\h&i\end{matrix}\right|&\left|\begin{matrix}a&c\\g&i\end{matrix}\right|&-\left|\begin{matrix}a&b\\g&h\end{matrix}\right|\\\left|\begin{matrix}b&c\\e&f\end{matrix}\right|&-\left|\begin{matrix}a&c\\d&f\end{matrix}\right|&\left|\begin{matrix}a&b\\d&e\end{matrix}\right|\end{pmatrix}$

Ejemplo

Obtener la adjunta de:

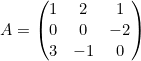
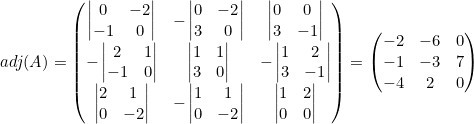
$A=\begin{pmatrix}1&2&1\\0&0&-2\\3&-1&0\end{pmatrix}$

$adj(A)=\begin{pmatrix}\left|\begin{matrix}0&-2\\-1&0\end{matrix}\right|&-\left|\begin{matrix}0&-2\\3&0\end{matrix}\right|&\left|\begin{matrix}0&0\\3&-1\end{matrix}\right|\\-\left|\begin{matrix}2&1\\-1&0\end{matrix}\right|&\left|\begin{matrix}1&1\\3&0\end{matrix}\right|&-\left|\begin{matrix}1&2\\3&-1\end{matrix}\right|\\\left|\begin{matrix}2&1\\0&-2\end{matrix}\right|&-\left|\begin{matrix}1&1\\0&-2\end{matrix}\right|&\left|\begin{matrix}1&2\\0&0\end{matrix}\right|\end{pmatrix}=\begin{pmatrix}-2&-6&0\\-1&-3&7\\-4&2&0\end{pmatrix}$