En este tema de tipos de matrices veremos:
Una tabla Excel, una tabla estadística o un simple sistema de ecuaciones son representaciones de datos que ya tienes asimiladas, pero en este tema empezamos a estudiar otra forma de representar los datos matemáticos: LAS MATRICES. Veamos qué son y qué tipos de matrices existen.
¿Qué es una matriz?
Una matriz es la representación de un conjunto de datos numéricos ordenados que podemos operar. Hasta aquí la parte estrictamente matemática. Entre tu y yo, las matrices son cosas de este tipo:
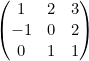
![]()
![]()
Como ves las matrices son una tabla de datos pero entre dos paréntesis y sin rayas, aunque realmente representan lo mismo.
Definiciones básicas de matrices
Dimensión de un matriz.
Lo primero que hay que saber de una matriz es su dimensión. La dimensión de una matriz es el número de filas y columnas que tiene y se expresa poniendo nº de filas ![]() nº de columnas.
nº de columnas.
![]()
La matriz A tiene 2 filas y 3 columnas, por lo que tiene una dimensión ![]()
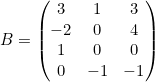
La matriz B tiene 4 filas y 3 columnas, por lo que tiene una dimensión ![]()
Matriz cuadrada.
Una matriz cuadrada es aquella matriz que tiene el mismo número de filas y columnas. Al ser el número de filas igual al de columnas, estas matrices no se dice que tengan una dimensión la que sea, sino que son de orden 2, 3, 4… siendo el orden de una matriz cuadrada el número de filas y columnas que tiene esta matriz. Las matrices cuadradas están entre los tipos de matrices, pero la introducimos para explicar los siguientes conceptos.
Ejemplo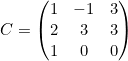
La matriz C tiene 3 columnas y 3 filas, por lo que tiene orden 3.
Diagonales en una matriz cuadrada.
La diagonal principal de una matriz es el conjunto de elementos que cruzan la matriz en diagonal y solo existe en las matrices cuadradas (mismo número de filas y columnas). La diagonal secundaria es la contraria y solo existe en matrices cuadradas.
Ejemplo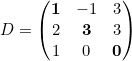
La matriz D tiene 3 filas y 3 columnas, por lo que se trata de una matriz cuadrada de orden 3. La diagonal principal son los números en negrita en la matriz de arriba. La diagonal secundaria son los números resaltados en la matriz de abajo.
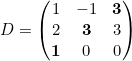
Matriz traspuesta.
La matriz traspuesta de otra matriz se obtiene cambiando las filas de la matriz del principio por columnas en la matriz traspuesta. Esta matriz no está entre los tipos de matrices aunque podría estarlo. La matriz traspuesta de ![]() se simboliza mediante
se simboliza mediante ![]()
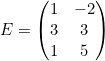
Para trasponer la matriz E o hallar Et tenemos que coger la primera fila de E y ponerla como si fuera la primera columna de la traspuesta. Tras esto repetimos el proceso con la segunda fila. Vamos, cambiar filas por columnas. La matriz Et quedaría de esta forma:
![]()
La matriz traspuesta tiene las siguientes propiedades:
Tipos de matrices.
Las matrices se pueden clasificar de muchas formas distintas. Vamos a ver las principales.
Tipos de matrices según su dimensión.
Si analizamos las matrices según la dimensión que tienen tenemos cuatros tipos de matrices:
- Matriz fila: es aquella que solo tiene una fila, es decir, su dimensión es 1
 n
n
![]()
- Matriz columna: es aquella que solo tiene una columna. Su dimensión es n
 1
1
![]()
- Matriz cuadrada: es aquella que tiene el mismo número de filas y columnas. Si tiene n filas y columnas decimos que es de orden n.
![Rendered by QuickLaTeX.com \[\begin{pmatrix} 1 & 3 & 1 \\ -2 & 3 & 5 \\ 2 & 1 & 0 \end{pmatrix}\]](https://www.motyscience.com/wp-content/ql-cache/quicklatex.com-130f7174071a2f5559dda928497a4379_l3.png)
- Matriz rectangular: aquella que tiene un número de filas y columnas desigual.
![]()
Tipos de matrices según su contenido.
- Matriz triangular: aquella matriz cuadrada que tiene todos los elementos por debajo o por encima de su diagonal principal son ceros. Si los ceros están por debajo de la diagonal principal se llama matriz triangular superior y si están por encima se denomina matriz triangular inferior.
TRIANGULAR SUPERIOR:

TRIANGULAR INFERIOR:
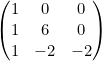
- Matriz diagonal: es una matriz cuadrada que tiene todo ceros menos la diagonal principal. Pueden existir matrices diagonales de todos los órdenes posibles (orden 2, 3, 4…).
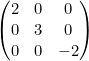
- Matriz escalar: es una matriz diagonal con todos los elementos de la diagonal principal iguales. Pueden existir matrices escalares de todos los órdenes (orden 2, 3, 4…).
![Rendered by QuickLaTeX.com \[\begin{pmatrix} -2 & 0 & 0 \\ 0 & -2 & 0 \\ 0 & 0 & -2 \end{pmatrix}\]](https://www.motyscience.com/wp-content/ql-cache/quicklatex.com-67ef6a7309563549e7a965ee6b49af17_l3.png)
- Matriz identidad: es una matriz escalar con todos los elementos de la diagonal principal iguales a 1. Se simboliza como
 ,
,  ,
,  …
…
ORDEN 2:
![]()
ORDEN 3:
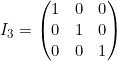
ORDEN 4:
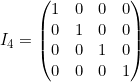
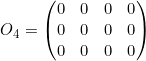
- Matriz nula: es una matriz cuadrada en la que todos los elementos son ceros. Dependiendo del orden de la matriz será más grande o más pequeña. Se simboliza como
 ,
,  ,
,  …
…
ORDEN 2:
![]()
ORDEN 3:
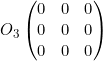
ORDEN 4: