Después de ver el campo magnético, podemos empezar a tratar la fuerza magnética. Esta es la segunda parte del tema de magnetismo y vamos a estudiar la fuerza ejercida por un campo magnético sobre:
¿Qué es la fuerza magnética?
La fuerza magnética es aquella que experimenta una carga o un elemento de carga al estar en presencia de un campo magnético. El vector fuerza magnética es siempre perpendicular al campo magnético en un punto.
Fuerza magnética experimentada por una carga puntual. Ley de Lorentz.
Cuando una carga puntual se mueve con una velocidad ![]() a través de un campo magnético
a través de un campo magnético ![]() experimenta una fuerza siguiendo la Ley de Lorentz.
experimenta una fuerza siguiendo la Ley de Lorentz.
![]()
Si analizamos este vector según su módulo, dirección y sentido podemos definir los siguientes puntos:
- El módulo del vector fuerza magnética que experimenta una carga viene dado por el módulo de la ley de Lorentz:
![]()
- La dirección del vector fuerza es perpendicular al vector campo.
- El sentido viene dado por la regla de la mano derecha. Si la carga es positiva, el sentido no varía, pero si la carga es negativa la fuerza magnética tiene sentido opuesto.
Regla de la mano derecha en el caso de fuerza ejercida sobre una carga.

En este caso la regla de la mano derecha se aplica de la siguiente forma:
- Se coloca la palma de la mano derecha con la dirección y el sentido de v.
- Se cierra la mano en dirección al vector B.
- ·El dedo pulgar (el dedo gordo) da el sentido del vector fuerza magnética.
Ejercicio resuelto de fuerza magnética.
Un protón p+, situado inicialmente en el origen de coordenadas, se mueve con
una velocidad inicial, ![]() , en presencia de un campo magnético uniforme
, en presencia de un campo magnético uniforme ![]() y de un campo eléctrico uniforme
y de un campo eléctrico uniforme ![]() . Determine la fuerza total sobre el electrón debida a los campos magnético y eléctrico, en el instante inicial.
. Determine la fuerza total sobre el electrón debida a los campos magnético y eléctrico, en el instante inicial.
Dato: Carga del protón, ![]() .
.
Lo primero, como siempre, es dibujar la situación con los datos que nos aporta el enunciado.

Una vez que lo tenemos dibujado vamos a dibujar las fuerzas magnética y eléctrica.

Como la partícula que se mueve es un electrón, es decir, que tiene carga negativa, la fuerza eléctrica irá en sentido contrario al campo y la fuerza magnética irá en sentido contrario a lo que saldría con la mano derecha, tal y como se ve en la imagen de arriba. Esto se debe a que tanto la fuerza eléctrica como la fuerza magnética está multiplicadas por la carga de electrón (carga negativa).
Tras obtener la dirección y el sentido de las fuerzas pasamos a calcular sus módulos.
![]()
![]()
![]()
![]()
![]()
![]()
La fuerza total, aplicando el principio de superposición para varias fuerzas, sería:
![]()
Fuerza magnética experimentada por un hilo. Ley de Laplace.
Cuando un hilo de longitud l por el que circula una intensidad I está en presencia de un campo magnético B el hilo experimenta una fuerza dada por:
![]()
Este vector tiene las siguientes características:
- El módulo del vector viene dado por la expresión:
![]()
- La dirección del vector fuerza es perpendicular al campo magnético y a la longitud del hilo.
- El sentido viene dado por la regla de la mano derecha.
Regla de la mano derecha en el caso de fuerza ejercida sobre un hilo.

En este caso la regla de la mano derecha se aplica de la siguiente forma:
- Se coloca la palma de la mano derecha con la dirección y el sentido de la intensidad del hilo I.
- Se cierra la mano en dirección al vector B.
- ·El dedo pulgar (el dedo gordo) da el sentido del vector fuerza magnética.
Fuerza por unidad de longitud entre dos hilos.
Muchas veces los hilos se consideran de longitud infinita, por lo que es muy común obtener el módulo de la fuerza magnética por unidad de longitud.
![]()
Cuando se tienen dos hilos de longitud infinita y se quiere calcular la fuerza que ejerce uno sobre el otro, se considera el campo creado por el primer hilo e introducirlo en la fórmula de la fuerza por unidad de longitud.
Si el campo generado por un hilo (llamemos a este hilo hilo 1) por el que circula una intensidad I1 es:
![]()
Y el módulo de la fuerza por unidad de longitud ejercida por el hilo 1 sobre el hilo 2 viene dada por la expresión:
![]()
Si se sustituye B por el campo generado por el hilo 1 se obtiene:
![]()
Ejercicio resuelto de fuerza magnética.
Dos conductores rectilíneos, paralelos y de longitud infinita, separados una distancia de 30cm están recorridos por corrientes eléctricas iguales de intensidad 2A. Determine el módulo de la fuerza por unidad de longitud que se ejercen entre sí estos conductores.
Dato: Permeabilidad magnética del vacío, ![]() .
.
Para obtener el módulo de la fuerza por unidad de longitud ejercida entre los dos hilos utilizamos directamente la fórmula que se ha demostrado en la parte de teoría de este punto y se sustituyen los datos para obtener el valor.
![]()
![]()
![]()
Fuerza magnética experimentada por una espira.
Una espira es un hilo enrollado tal y como se ve en la imagen. Las espiras pueden ser cuadradas o circulares. Si una espira está en presencia de un campo magnético experimentará una fuerza nula, es decir, igual a cero. Esto último se debe a que la fuerza que se hace sobre un lado de la espira es de igual módulo y dirección, pero de sentido contrario a la que experimenta el lado opuesto.


Por el contrario, cuando la espira está en presencia de un campo magnético se genera un momento. La fuerza ejercida sobre los lados superior e inferior es cero, dado que el vector campo magnético y el vector longitud son paralelos, mientras que la suma de las fuerzas sobre los laterales derecho e izquierdo de la espira es cero. Estas fuerzas no se ejercen sobre el mismo punto, por lo que la espira rota, pero no cambia su posición en el espacio al no existir fuerza. Esto es debido al momento que se genera cuando dos fuerzas contrarias no se aplican sobre el mismo punto.
Momento de una espira.
Las fuerzas que experimenta la espira en sus lados derecho e izquierdo se denominan par de fuerzas. Un par de fuerzas son dos fuerzas con el mismo módulo y dirección, pero sentidos opuestos con un punto de aplicación distinto.
El momento de fuerza ejercido sobre una espira es un vector con las siguientes características:
- El módulo del momento viene dado por la expresión:
![]()
- La dirección del momento es perpendicular a los vectores
 y
y  .
. - El sentido lo da la regla de la mano derecha tal y como ocurre con la fuerza magnética y los vectores
 y
y 
Todo esto se resume en la siguiente fórmula matemática:
![]()
De esta fórmula se puede extraer el momento magnético de una espira. Este momento es independiente del valor del campo, por lo que queda:
![]()
Cuando existen varias espiras superpuestas el momento magnético queda de la siguiente forma:
![]()
Si introducimos el momento magnético en la expresión del momento de fuerza ejercido sobre una espira de corriente queda:
![]()

Por último creo que es necesario definir la dirección y el sentido del vector superficie. La dirección del vector superficie es perpendicular al plano en el que se sitúa la espira. El sentido lo da la regla de la mano derecha como es ve en la animación.
Ejercicio resuelto del momento de una espira.
Una espira cuadrada de 10 cm de lado está recorrida por una corriente eléctrica constante de 30 mA. Determine el momento magnético de la espira.
SoluciónLo primero, como siempre, es dibujar la situación con los datos que nos aporta el enunciado.
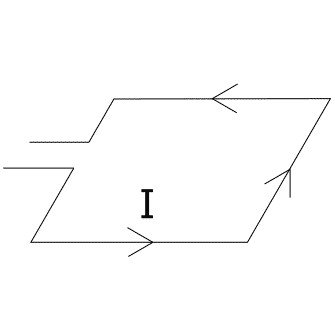
Para obtener el momento magnético de la espira utilizamos la fórmula que tenemos en la parte de teoría para momento de una espira.
![]()
![]()
![]()










