Equilibrio químico. Apuntes y ejercicios resueltos.

El equilibrio químico es el tema en el que se basan los dos siguientes temas: equilibrio de solubilidad y ácido-base.

Partes del tema:

¿Qué es el equilibrio químico?

Tabla del equilibrio químico.

La constante del equilibrio químico (K).

Cinética química

Equilibrio de solubilidad

Cociente de la reacción (Q).

Grado de disociación.

Factores que influyen en el estado de equilibrio. Principio de Le Chatelier.

¿Qué es el equilibrio químico?

En la inmensa mayoría de reacciones químicas se crea un flujo circular en el que los reactivos se convierten en productos y los productos se convierten en reactivos.

Cuando una reacción química comienza solo hay reactivos y poco a poco se van generando productos. En este momento, la velocidad a la que se generan los productos (velocidad directa) es muy elevada, mientras que la velocidad a la que se vuelven a crear reactivos (velocidad inversa) es muy baja. Con el paso del tiempo la velocidad directa e inversa se igualan y se forma el equilibrio químico.

Una reacción alcanza el equilibrio químico cuando la velocidad directa es igual que la velocidad inversa. Esto se puede apreciar en el siguiente gráfico.

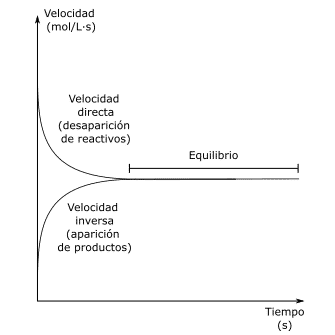
Gráfica en la que se ve como las velocidades directa e inversa se igualan, alcanzando el equilibrio químico

Al alcanzar el equilibrio químico, las concentraciones cada uno de los reactivos y productos son constantes.

Para estudiar el equilibrio químico se utiliza una tabla de equilibrio. En esta tabla se estudian el momento inicial y la situación de equilibrio.

Tabla del equilibrio químico.

Las tablas de equilibrio pueden estudiarse con concentraciones, número de moles y presiones.

En el momento inicial solo solo tenemos reactivos (por lo general), por lo que los productos son cero. Esta parte sería la primer fila de la tabla.

Conforme pasa el tiempo la reacción genera productos, por lo que una cantidad x se convierte en productos y deja de ser reactivos. Esta parte sería la segunda fila de la tabla. En esta segunda fila se resta esta cantidad x multiplicada por el coeficiente estequiométrico correspondiente a cada cantidad inicial de reactivos y se suma a los productos.

Para una reacción del tipo $aA+bB\rightleftharpoons+cC+dD$ las tablas de equilibrio químico con concentraciones, número de moles y presiones serían así:

Tabla de equilibrio con concentraciones.

	aA+	bB	$\rightleftharpoons$	cC+	dD
Concentraciones iniciales	C_oA	C_oB		0	0
Concentraciones en el equilibrio	C_oA-ax	C_oB-bx		cx	dx

Tabla de equilibrio con moles.

	aA+	bB	$\rightleftharpoons$	cC+	dD
Número de moles iniciales	n_A	n_B		0	0
Número de moles en el equilibrio	n_A-an_x	n_B-bn_x		cn_x	dn_x

Tabla de equilibrio con presiones.

	aA+	bB	$\rightleftharpoons$	cC+	dD
Presiones iniciales	p_A	p_B		0	0
Presiones en el equilibrio	p_A-ap_x	p_B-bp_x		cp_x	dp_x

Ejercicios resueltos tabla de equilibrio.

Para las siguientes reacciones obtén la tabla de equilibrio.

a) $PCl_5(g)\rightleftharpoons{PCl_3}(g)+Cl_2(g)$ (con concentraciones).

b) $N_2O_4(g)\rightleftharpoons2NO_2(g)$ (con presiones).

c) $2H_2O(g)\rightleftharpoons2H_2(g)+O_2(g)$ (con número de moles).

d) $Sb_2O_5(g)\rightleftharpoons{S}b_2O_3 (g)+O_2(g)$ (con concentraciones).

Solución

a) $PCl_5(g)\rightleftharpoons{PCl_3}(g)+Cl_2(g)$ (con concentraciones).

	PCl₅	$\rightleftharpoons$	PCl₃+	Cl₂
Concentraciones iniciales	C_o		0	0
Concentraciones en el equilibrio	C_o-x		x	x

b) $N_2O_4(g)\rightleftharpoons2NO_2(g)$ (con presiones).

	N₂O₄	$\rightleftharpoons$	2NO₂+
Presiones iniciales	p_o		0
Presiones en el equilibrio	p_o-p_x		2p_x

c) $2H_2O(g)\rightleftharpoons2H_2(g)+O_2(g)$ (con número de moles).

	2H₂O	$\rightleftharpoons$	2H₂+	O₂
Número de moles iniciales	n_o		0	0
Número de moles en el equilibrio	n_o-2n_x		2n_x	n_x

d) $Sb_2O_5(g)\rightleftharpoons{S}b_2O_3 (g)+O_2(g)$ (con concentraciones).

	Sb₂O₅	$\rightleftharpoons$	Sb₂O₃+	O₂
Concentraciones iniciales	C_o		0	0
Concentraciones en el equilibrio	C_o-x		x	x

La constante de equilibrio químico.

La constante de equilibrio es una forma de relacionar la cantidad de reactivos y productos en una reacción. Cuanto mayor sea esta constante, más cantidad de productos se generará.

La constante de equilibrio solo depende de la temperatura, por lo que si tenemos una reacción a cierta temperatura, la constante de equilibrio no variará a no ser que cambie la temperatura.

Cada constante de equilibrio tiene sus propias unidades dependiendo de la reacción química que se estudie, es decir, las unidades de la constante de equilibrio se obtienen de la expresión. Normalmente estas unidades no se suelen poner por el hecho de ser variables.

En las constantes de equilibrio solo se introducen sustancias gaseosas o en disolución acuosa y se introducen los datos en el equilibrio.

Formas de expresar la constante de equilibrio.

Tal y como ocurre con las tablas de equilibrio, también se puede expresar de diferentes formas la constante de equilibrio.

Constante de concentraciones K_c.

La constante de equilibrio referida a las concentraciones para una reacción $aA(g)+bB(g)\rightleftharpoons cC(g)+dD(g)$ tiene esta forma:

$\left.K_c=\dfrac{[C]^c[D]^d}{[A]^a[B]^b}\right\}_{eq}$

En la constante de equilibrio solo se incluyen aquellos productos o reactivos que estén en estado gaseoso o en disolución acuosa. Las concentraciones que se introducen en esta fórmula deben ser las que hay en el equilibrio.

Cuando la constante de concentraciones es inferior a 10^-3 se desprecia el valor de la cantidad x que pasa de reactivos a productos.

Demostración de la K_c

La constante de equilibrio químico referida a las concentraciones se obtiene con el concepto de equilibrio. El equilibrio químico se alcanza cuando la velocidad directa es igual que la velocidad inversa. Si igualamos las velocidades obtenemos la constante de concentraciones de esta manera.

$\left.\begin{matrix}v_d=k_d[A]^a[B]^b\\v_i=k_i[C]^c[D]^d\end{matrix}\right\}\longrightarrow\dfrac{v_d}{v_i}=\dfrac{k_d}{k_i}\dfrac{[A]^a[B]^b}{[C]^c[D]^d}\longrightarrow1=\dfrac{k_d}{k_i}\dfrac{[A]^a[B]^b}{[C]^c[D]^d}$

$\dfrac{k_d}{k_i}=\dfrac{[C]^c[D]^d}{[A]^a[B]^b}=K_c$

Ejemplo de obtención de la concentración x que pasa de reactivos a productos.

A 2600 K se introduce 1 mol de agua en un recipiente vacío de 100 L, alcanzándose el siguiente equilibrio: $2H_2O(g)\rightleftharpoons2H_2 (g) + O_2 (g)$ , con $K_c=1'97\cdot10^{-7}$ . Calcule el número de moles de O₂ en el equilibrio.

Solución

El primer paso para resolver un ejercicio de equilibrio es hacer la tabla del equilibrio. En este caso la haremos para las concentraciones dado que nos dan como dato K_c.

Para conseguir la tabla hay que obtener la concentración inicial de vapor de agua dividiendo los moles de agua entre el volumen expresado en litros (recuerda que la concentración se expresa en molaridad).

$C_o=\dfrac{n(H_2O)}{V_D(L)}=\dfrac{1mol}{100L}=0'01M$

	2H₂O (g)	$\rightleftharpoons$	2H₂ (g) +	O₂ (g)
Número de moles iniciales	C_o		0	0
Número de moles en el equilibrio	0’01-2x		2x	x

Una vez que hemos obtenido la tabla hallamos la expresión de K_c para conseguir la concentración de O₂ que se producen.

$K_c=\dfrac{[H_2]^2[O_2]}{[H_2O]^2}=\dfrac{(2x)^2\cdot x}{(0'01-2x)^2}$

Como la Kc es inferior a 10-3 se puede despreciar el valor de la x del denominador y, sustituyendo la Kc en la expresión anterior quedaría:

$1'97\cdot10^{-7}=\dfrac{(2x)^2\cdot x}{0'01^2}$

Una vez obtenida esta ecuación despejamos x, que es la concentración de O₂ en el equilibrio.

$1'97\cdot10^{-7}=\dfrac{4x^3}{0'01^2}\longrightarrow4x^3=\cdot1'97\cdot10^{-7}\cdot10^{-4}\longrightarrow x^3=\dfrac{1'97\cdot10^{-11}}{4}$

$x=\pm\sqrt[3]{4'925\cdot10^{-12}}=1'7\cdot10^{-4}mol/L$

En el caso de que esta ecuación tuviera dos soluciones, una positiva y otra negativa, nosotros solo cogemos la positiva, dado que no se puede obtener como resultado una concentración negativa.

Después de obtener la concentración hayamos el número de moles con la fórmula de la concentración.

$n=x\cdot V=1'7\cdot10^{-4}mol/l\cdot100L=0'017mol$

Constante de presiones K_p.

La constante de equilibrio también puede expresarse en función de las presiones parciales de cada reactivo y producto cuando se alcanza el equilibrio.

Para la reacción $aA(g)+bB(g)\rightleftharpoons cC(g)+dD(g)$ se obtiene una constante de presiones:

$\left.K_p=\dfrac{P_C^cP_D^d}{P_A^aP_B^b}\right\}_{eq}$

En la constante de equilibrio solo se incluyen aquellos productos o reactivos que estén en estado gaseoso o en disolución acuosa. Las presiones parciales que se introducen en esta fórmula deben ser las que hay en el equilibrio.

Ejercicio cálculo de K_p.

Se introducen 25’6 g de SO₂ y 0,2 mol de O₂ gaseosos en un recipiente de 1 L a 850 K. Tras
alcanzarse el equilibrio $SO_2(g)+\dfrac{1}{2}O_2(g)\rightleftharpoons SO_3(g)$ , se encuentra que la concentración de producto es 0,37 M.

a) Determine la presión parcial de cada gas en el equilibrio.

b) Calcule Kp.

Datos: $R=0'082atm\cdot L\cdot mol^{-1}\cdot K^{-1}$ ; masas molares: $O=16g/mol$ , $S=32g/mol$ .

Solución

a) El primer paso para resolver un ejercicio de equilibrio es hacer la tabla del equilibrio. En este caso la haremos para el número de moles dado que no nos dan la presión total.

Para conseguir la tabla de equilibrio hay que calcular antes el número de moles del SO₂.

$n(SO_2)=\dfrac{m(SO_2)}{Mm(SO_2)}=\dfrac{25'6mol}{64}=0'4mol$

En el enunciado nos dicen que la concentración de producto es 0’37M, es decir, que el número de moles de producto (O₂) es 0’37 mol también porque el volumen es 1L. Esto supone que n_x es 0’37 mol.

	SO₂ (g)	1/2 O₂	$\rightleftharpoons$	SO₃ (g)
Número de moles iniciales	0’4	0’2		0
Número de moles en el equilibrio	0’4- 0’37 = = 0’03	0’2 – 1/2 · 0’37 = = 0’015		0’37

Tras esto calculamos las presiones parciales de cada gas en el equilibrio utilizando la ley de los gases ideales, introduciendo el número de moles en el equilibrio de cada gas.

$P_{SO_2}=\dfrac{n_{SO_2}RT}{V}=\dfrac{0'03mol\cdot0'082atm\cdot L\cdot mol^{-1}\cdot K^{-1}\cdot850K}{1L}=2'1atm$

$P_{O_2}=\dfrac{n_{O_2}RT}{V}=\dfrac{0'015mol\cdot0'082atm\cdot L\cdot mol^{-1}\cdot K^{-1}\cdot850K}{1L}=1'05atm$

$P_{SO_3}=\dfrac{n_{SO_3}RT}{V}=\dfrac{0'37mol\cdot0'082atm\cdot L\cdot mol^{-1}\cdot K^{-1}\cdot850K}{1L}=25'8atm$

b) Una vez halladas las presiones en el equilibrio solo hay que introducirlas en la expresión de K_p para obtener la constante de equilibrio.

$K_p=\dfrac{P_{SO_3}}{P_{SO_2}\cdot P^{1/2}_{O_2}}=\dfrac{25'8atm}{2'1atm\cdot(1'05atm)^{1/2}}=12atm^{-1}$

Relación entre K_c y K_p.

Ambas constantes se pueden relacionar para sacar una a partir de la otra con la siguiente expresión.

$K_p=K_c(RT)^{\Delta n}$

En esta expresión R es la constante de los gases ideales, T es la temperatura en Kelvins y $\Delta n$ es la variación de número de moles gaseosos.

Para obtener el valor de $\Delta n$ se suman los coeficientes estequiométricos de los productos gaseosos de la reacción y se restan con la suma de los reactivos. Para una reacción genérica como $aA(g)+bB(g)\rightleftharpoons cC(g)+dD(g)$ quedaría:

$\Delta n=(c+d)-(a+b)$

Ejercicio relación entre K_c y K_p.

A 2600 K se introduce 1 mol de agua en un recipiente vacío de 100L, alcanzándose el
siguiente equilibrio: $2H_2O (g)\rightleftharpoons2H_2(g)+O_2(g)$ , con $K_p=4'2\cdot10^{-5}$ . Calcule Kc.

Dato: $R=0'082atm\cdot L\cdot mol^{-1}\cdot K^{-1}$ .

Solución

Para obtener el valor de K_c es tan fácil como despejar y sustituir los datos que nos dan en la expresión:

$K_p=K_c(RT)^{\Delta n}=\longrightarrow K_c=\dfrac{K_p}{(RT)^{\Delta n}}$

En este caso tenemos que $\Delta n=2+1-2=1$ , por lo que al sustituir los datos en la expresión queda que K_c es:

$K_c=\dfrac{K_p}{(RT)^{\Delta n}}=\dfrac{4'2\cdot10^{-5}}{(0'082atm\cdot L\cdot mol^{-1}\cdot K^{-1}\cdot2600K)^1}=1'97\cdot10^{-7}$

Cociente de la reacción (Q).

El valor de la constante de equilibrio nos da una referencia para conocer que ocurre cuando la reacción está en el equilibrio. Si analizamos una reacción ya comenzada, no sabemos si está en equilibrio o no. Para averiguar que ocurrirá con las cantidades de productos y reactivos al analizar una reacción utilizamos el cociente de reacción.

El cociente de reacción (Q) tiene la misma expresión que la constante de equilibrio pero las concentraciones o las presiones no se encuentran en el equilibrio.

$Q_c=\dfrac{[C]^c[D]^d}{[A]^a[B]^b}$

$Q_p=\dfrac{P_C^cP_D^d}{P_A^aP_B^b}$

La reacción siempre va a intentar estar en equilibrio. De esta forma, si hay más productos de los que debería haber en el equilibrio, la reacción generará más reactivos (se desplaza hacia los reactivos), mientras que si tiene mayor cantidad de reactivos, generará más productos (se desplaza hacia los productos).

Si Q > K, la reacción se desplaza hacia los reactivos.
Si Q < K, la reacción se desplaza hacia los productos.
En el caso de Q = K, la reacción estará en equilibrio.

Grado de disociación.

El grado de disociación se entiende por el porcentaje de reactivos que pasan a ser productos. Este dato nos dice cuánto está desplazada la reacción hacia los productos, es decir, el rendimiento.

El grado de disociación se puede obtener de tres formas distintas dependiendo de los datos que nos aporte el enunciado.

Concentraciones.

$\alpha=\dfrac{x}{C_o}$

Número de moles.

$\alpha=\dfrac{n_x}{n_o}$

Presiones.

$\alpha=\dfrac{p_o}{p_x}$

Este nuevo elemento en el equilibrio hace que las tablas puedan expresarse en función del grado de disociación sustituyendo los valores de x, n_x y p_x por la expresión correspondiente. La tabla de equilibrio para las concentraciones (para el número de moles y para las presiones son iguales) quedaría:

	aA+	bB	$\rightleftharpoons$	cC+	dD
Concentraciones iniciales	$C_{o_A}$	$C_{o_B}$		0	0
Concentraciones en el equilibrio	$C_{o_A}-ax$	$C_{o_B}-bx$		$cx$	$dx$
Concentraciones en el equilibrio (grado de disociación)	$C_{o_A}(1-a\alpha)$	$C_{o_B}(1-b\alpha)$		$cC_o\alpha$	$dC_o\alpha$

En esta tabla se ha sustituido x por C_oα en la última fila.

Ejercicio obtención del grado de disociación.

A 30ºC se introducen 138 g de N₂O₄ en un matraz de 50 L, transcurriendo la siguiente reacción: $N_2O_4(g)\rightleftharpoons2NO_2(g)$ , con $K_p=0'21$ .

a) Escriba equilibrio, exprese el número de moles en equilibrio de cada compuesto en función del grado de disociación.

b) Obtenga el grado de disociación.

Datos: masas atómicas: $N=14$ , $O=16$ ; $R=0'082atm\cdot L\cdot mol^{-1}\cdot K^{-1}$ .

Solución

a) Lo primero, como en todos los ejercicios de equilibrio es obtener la tabla de equilibrio. En este caso nos dan la masa de N₂O₄, por lo que pasaremos esta masa a moles y escribiremos la tabla con número de moles (por que lo pide el enunciado) y concentraciones (para obtener el grado de disociación).

$n(N_2O_4)=\dfrac{m}{Mm}=\dfrac{138g}{92g/mol}=1'5mol$

	N₂O₄ (g)	$\rightleftharpoons$	2NO₂ (g)
Número de moles iniciales	$1'5$		$0$
Número de moles en el equilibrio	$1'5-n_x=1'5(1-\alpha)$		$2n_x=3\alpha$
Concentración en el equilibrio	$\dfrac{1'5}{50}(1-\alpha)=0'03(1-\alpha)$		$\dfrac{3}{50}\alpha=0'06\alpha$

El número de moles en el equilibrio de NO₂ en función del grado de disociación se obtiene haciendo $2n_o\alpha=2\cdot1'5\alpha=3\alpha$

b) Para obtener el valor del grado de disociación utilizamos la K_c. Para obtener la K_c utilizamos la relación que existe entre esta constante y K_p que es la que nos dan en el enunciado.

$K_p=K_c(RT)^{\Delta n}\longrightarrow K_c=\dfrac{K_p}{(RT)^{\Delta n}}$

$K_c=\dfrac{0'21}{(0'082atm\cdot L\cdot mol^{-1}\cdot K^{-1}(30+273))^{(2-1)}}=0'0085$

Una vez que tenemos el valor de K_c podemos despejar el grado de disociación de la expresión de K_c (recuerda que hay que poner las concentraciones en esta constante).

$K_c=\dfrac{(0'06\alpha)^2}{0'03(1-\alpha)}\rightarrow0'0085=\dfrac{0'0036\alpha^2}{0'03(1-\alpha)}\rightarrow$

$\rightarrow0'0000255-0'000255\alpha=0'0036\alpha^2$

$3'6\cdot10^{-3}\alpha^2+2'55\cdot10^{-4}\alpha-2'55\cdot10^{-4}=0\longrightarrow\left\{\begin{matrix}\alpha=0'23\\\alpha=-0'3\end{matrix}\right.$

Descartamos la opción de abajo por ser negativa. De esta forma, el grado de disociación será $\alpha=0'23$ , es decir, que la reacción está disociada en un 23%.

Factores que alteran el equilibrio. Principio de Le Chatelier.

El principio de Le Chatelier es la herramienta que existe en equilibrio químico para predecir lo que ocurrirá en el equilibrio cuando se modifican las condiciones en las que se da el equilibrio.

Según el principio de Le Chatelier, la reacción va a tender a contrarrestar las modificaciones que se generen en el equilibrio.

Ante una modificación externa de factores que modifican el equilibrio, el sistema evolucionará oponiéndose a dicha modificación.
Principio de le châtelier.

Las condiciones que pueden modificarse en un equilibrio químico son:

Presión.

Cuando se aumenta la presión la reacción tenderá a disminuir la presión para alcanzar de nuevo el equilibrio. Esta disminución de presión se consigue disminuyendo el número de moles de la reacción (utilizando la ley de los gases ideales). Para dismunuir el número de moles en el equilibrio la reacción se desplazará en el sentido en el que menor número de moles haya. Por otro lado cuando disminuye la presión, la reacción se desplaza hacia donde mayor número de moles haya.

Si la presión aumenta la reacción se desplaza hacia donde haya menor número de moles gaseosos.

Si la presión disminuye la reacción se desplaza hacia donde haya mayor número de moles gaseosos.

En el caso de tener el mismo número de moles gaseosos a ambos lados de la reacción, esta no experimentará ningún cambio.

Ejemplos

Si en la reacción $N_2O_4(g)\rightleftharpoons2NO_2(g)$ aumentamos la presión, la reacción se desplazará hacia los reactivos, dado que por cada mol que haya de reactivos hay dos moles de producto. Esto puede verse con los coeficientes estequiométricos. Reactivos: 1; productos: 2.
Si en la reacción $2H_2(g)+O_2(g)\rightleftharpoons2H_2O(g)$ disminuimos la presión, la reacción se desplazará hacia los reactivos, dado que por cada tres moles que hay de reactivos hay dos moles de producto. Reactivos: 3; productos: 2.
Si en la reacción $CH_4(g)+2O_2(g)\rightleftharpoons CO_2(g)+2H_2O(g)$ disminuimos o aumentamos la presión, la reacción no experimentará ningún cambio, dado que el número de moles gaseosos en los productos y en los reactivos es el mismo. Reactivos: 3; productos: 3.

Temperatura.

Cuando se modifica la temperatura, la reacción va a desplazarse oponiéndose al cambio de temperatura. Para saber hacia dónde se desplaza una reacción vamos primero a repasar los conceptos de reacción endotérmica y exotérmica.

Una reacción es endotérmica cuando los productos son más energéticos que los reactivos ( $\Delta H>0$ ), mientras que una reacción es exotérmica cuando los reactivos son más energéticos que los productos ( $\Delta H<0$ ). Esto puede observarse en los siguientes diagramas entálpicos.

Si se aumenta la temperatura de una reacción, esta se desplazará en el sentido en el que sea endotérmica.

Si se disminuye la temperatura de una reacción, esta se desplazará en el sentido en el que sea exotérmica.

Ejemplo

La reacción $2H_2O(g)\rightleftharpoons2H_2(g)+O_2(g)$ es endotérmica, es decir, $\Delta H>0$ . Si aumentamos la temperatura de esta reacción, la reacción se desplazará hacia los productos.
La reacción $CH_4(g)+2O_2(g)\rightleftharpoons CO_2(g)+2H_2O(g)$ es exotérmica, es decir, $\Delta H>0$ . Si aumentamos la temperatura de esta reacción, la reacción se desplazará hacia los reactivos. Esto se debe a que si en el sentido directo es exotérmica, en el sentido inverso es endotérmica.

Concentraciones de reactivos o productos.

Cuando se modifican las concentraciones de los reactivos o los productos de una reacción química, se altera la constante de concentraciones.

Si se aumenta la concentración de uno o más reactivos, la reacción se desplazará hacia los productos.

Si se aumenta la concentración de uno o más productos, la reacción se desplazará hacia los reactivos.

Ejemplo

Aumentamos la concentración de H₂ en la reacción $2H_2O(g)\rightleftharpoons2H_2(g)+O_2(g)$ . Esta reacción se desplazará hacia los reactivos para oponerse a la modificación.
Si aumentamos la concentración de H₂O en la misma reacción que en el caso anterior, la reacción se desplazará hacia los productos.

Volumen.

Al modificar el volumen se modifica la presión de la reacción, por lo que tendrá el mismo efecto que cuando se modifica la presión pero en sentido inverso (esto se debe a la ley de los gases ideales).

Si se aumenta el volumen de una reacción, el equilibrio se desplaza hacia donde haya mayor número de moles gaseosos.

Si se disminuye el volumen de una reacción, el equilibrio se desplaza hacia donde haya menor número de moles gaseosos.

En el caso de tener el mismo número de moles gaseosos a ambos lados de la reacción, esta no experimentará ningún cambio.

Ejemplo

Si aumentamos el volumen en la reacción $N_2O_4(g)\rightleftharpoons2NO_2(g)$ , esta se desplazará exactamente igual que si disminuyéramos la presión, por lo que se desplazaría hacia los productos.
Si por el contrario disminuyéramos el volumen, la reacción se desplazaría de la misma forma que si aumentáramos la presión, es decir, hacia los reactivos.

Catalizadores.

Los catalizadores no modifican el equilibrio químico, dado que su única función es acelerar o ralentizar la velocidad de una reacción.

Ejercicios resueltos de equilibrio químico.

A continuación es recomendable intentar resolver estos problemas resueltos de equilibro químico para coger práctica en la materia.

Ejercicio de equilibrio químico 1.

A 400ºC, en un recipiente de 5 L se introduce 1’2 mol de CO₂ y 0’75 mol de H₂. Una vez alcanzado el equilibrio: $CO_2(g)+H_2(g)\rightleftharpoons CO(g)+H_2O(g)$ se analiza la mezcla y se encuentra que hay 0’6 mol de CO₂.

a) Calcule la concentración de cada especie en el equilibrio.

b) Determine el valor de las constantes K_c y K_p.

c) Calcule la presión total del sistema en equilibrio.

d) Justifique, sin cálculos, cómo se altera el equilibrio:

si se añade 1 mol más de CO2
si en lugar de 5 L, se reduce el volumen a 1 L.

Dato: $R=0'082atm\cdot{L}\cdot{mol}^{-1}\cdot{K}^{-1}$ .

Solución

Estamos trabajando para traerte la solución de este ejercicio.

–

Ejercicio de equilibrio químico 2.

A 30ºC se introducen 138g de N₂O₄ en un matraz de 50L, transcurriendo la siguiente reacción: $N_2O_4(g)\rightleftharpoons2NO_2(g)$ , con $K_p=0'21$ .

a) Escriba el equilibrio y exprese el número de moles en equilibrio de cada compuesto en función del grado de disociación.

b) Obtenga el grado de disociación.

c) Justifique, sin realizar cálculos, si el grado de disociación aumenta, disminuye o permanece constante cuando la reacción tiene lugar a la misma temperatura, pero a menor presión.

Datos: Masas atómicas: $N=14$ ; $O=16$ . $R=0'082atm\cdot{L}\cdot{mol}^{-1}\cdot\cdot{K}^{-1}$ .

Solución

Estamos trabajando para traerte la solución de este ejercicio.

–

Ejercicio de equilibrio químico 3.

En un reactor químico a 182ºC y 1atm de presión el SbCl₅ está disociado en un 29,2% según la reacción: $SbCl_5(g)\rightleftharpoons{Sb}Cl_3(g)+Cl_2(g)$ .

a) Calcule las presiones parciales de cada gas en el equilibrio.

b) Calcule las constantes de equilibrio K_p y K_c.

c)Justifique si se modifica el equilibrio al realizar la reacción a la misma temperatura y a una presión menor de 1atm.

d)Indique si se modifica el equilibrio al añadir un catalizador. Justifique la respuesta.

Dato: $R=0'082atm\cdot{L}\cdot{mol}^{-1}\cdot\cdot{K}^{-1}$ .

Solución

Estamos trabajando para traerte la solución de este ejercicio.

–

Ejercicio de equilibrio químico 4.

En un recipiente cerrado, se calienta a 182 ºC pentacloruro de arsénico gaseoso que se disocia en tricloruro de arsénico gaseoso y en cloro molecular. En el equilibrio y a una presión total de 1 atm, el pentacloruro de arsénico se disocia un 29’2 %. Calcule:

a) Las presiones parciales de los tres gases en el equilibrio.

b) Kc y Kp.

c) Las concentraciones molares de todas las sustancias en el equilibrio.

Dato: $R=0'082atm\cdot{L}\cdot{mol}^{-1}\cdot\cdot{K}^{-1}$ .

Solución

Estamos trabajando para traerte la solución de este ejercicio.

–

Ejercicio de equilibrio químico 5.

En un reactor de 20 L, una mezcla gaseosa constituida inicialmente por 7 mol de hidrógeno y 5 mol de yodo, se calienta a 350 ºC. En el equilibrio, $H_2(g)+I_2(g)\rightleftharpoons2HI(g)$ , hay 8’6 mol de yoduro de hidrógeno gaseoso. La entalpía de la reacción es ∆H = −10,83 kJ.

a) Indique cómo se modifica el equilibrio al aumentar la temperatura.

b) Calcule la constante de equilibrio Kc.

c) Calcule la presión parcial de hidrógeno en el equilibrio.

Dato: $R=0'082atm\cdot{L}\cdot{mol}^{-1}\cdot\cdot{K}^{-1}$ .

Solución

Estamos trabajando para traerte la solución de este ejercicio.

–

$\text{}$

Cinética química

Equilibrio de solubilidad

Equilibrio químico. Apuntes y ejercicios resueltos.

¿Qué es el equilibrio químico?

Tabla del equilibrio químico.

Tabla de equilibrio con concentraciones.

Tabla de equilibrio con moles.

Tabla de equilibrio con presiones.

Ejercicios resueltos tabla de equilibrio.

La constante de equilibrio químico.

Formas de expresar la constante de equilibrio.

Constante de concentraciones K_c.

Ejemplo de obtención de la concentración x que pasa de reactivos a productos.

Constante de presiones K_p.

Ejercicio cálculo de K_p.

Relación entre K_c y K_p.

Ejercicio relación entre K_c y K_p.

Cociente de la reacción (Q).

Grado de disociación.

Ejercicio obtención del grado de disociación.

Factores que alteran el equilibrio. Principio de Le Chatelier.

Presión.

Temperatura.

Concentraciones de reactivos o productos.

Volumen.

Catalizadores.

Ejercicios resueltos de equilibrio químico.

Ejercicio de equilibrio químico 1.

Ejercicio de equilibrio químico 2.

Ejercicio de equilibrio químico 3.

Ejercicio de equilibrio químico 4.

Ejercicio de equilibrio químico 5.

¿Nos mantenemos en contacto?

Traba con nosotros

TRABAJA EN MOTYSCIENCE

¿Qué es el equilibrio químico?

Tabla del equilibrio químico.

Tabla de equilibrio con concentraciones.

Tabla de equilibrio con moles.

Tabla de equilibrio con presiones.

Ejercicios resueltos tabla de equilibrio.

La constante de equilibrio químico.

Formas de expresar la constante de equilibrio.

Constante de concentraciones Kc.

Ejemplo de obtención de la concentración x que pasa de reactivos a productos.

Constante de presiones Kp.

Ejercicio cálculo de Kp.

Relación entre Kc y Kp.

Ejercicio relación entre Kc y Kp.

Cociente de la reacción (Q).

Grado de disociación.

Ejercicio obtención del grado de disociación.

Factores que alteran el equilibrio. Principio de Le Chatelier.

Presión.

Temperatura.

Concentraciones de reactivos o productos.

Volumen.

Catalizadores.

Ejercicios resueltos de equilibrio químico.

Ejercicio de equilibrio químico 1.

Ejercicio de equilibrio químico 2.

Ejercicio de equilibrio químico 3.

Ejercicio de equilibrio químico 4.

Ejercicio de equilibrio químico 5.

¿Nos mantenemos en contacto?

Traba con nosotros

TRABAJA EN MOTYSCIENCE

Constante de concentraciones K_c.

Constante de presiones K_p.

Ejercicio cálculo de K_p.

Relación entre K_c y K_p.

Ejercicio relación entre K_c y K_p.