Propiedades de los determinantes. ¿Cuáles son?

Ya podemos calcular cualquier determinante, pero como has podido observar el proceso para desarrollar un determinante es bastante complejo y cuando empiezas a subir de orden se va complicando exponencialmente. Las propiedades de los determinantes nos facilitan el cálculo y nos van a ayudar también en otros aspectos como el cálculo del rango de una matriz o la discusión de un sistema en futuros temas.

Propiedades de los determinantes.

El determinante que tiene una de sus filas o columnas formada por todo ceros es igual a cero.

Ejemplo

$\left|\begin{matrix}1&1&2\\0&0&0\\2&1&3\end{matrix}\right|=0$

$\left|\begin{matrix}1&0&2\\1&0&1\\-2&0&2\end{matrix}\right|=0$

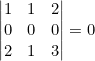
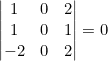
El determinante que tiene dos filas o columnas iguales o proporcionales es cero.

Ejemplo

$\left|\begin{matrix}1&1&2\\2&2&4\\2&1&3\end{matrix}\right|=0$ $\longrightarrow$ $F_2=2F_1$

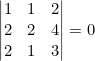
Cuando una fila o columna es una combinación lineal de otras filas o columnas el determinante es cero.

Ejemplo

$\left|\begin{matrix}1&1&2\\1&2&-1\\3&4&3\end{matrix}\right|=0$ $\longrightarrow$ $F_3=2F_1+F_2$

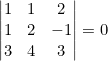
Si en un determinante se suma a una fila o columna una combinación lineal de las otras filas o columnas el determinante se multiplica por (-1).

Ejemplo

$\left|\begin{matrix}1&-1&2\\0&2&-1\\-3&1&1\end{matrix}\right|=12\longrightarrow F_2=F_2+2F_1$ $\longrightarrow\left|\begin{matrix}1&-1&2\\2&0&3\\-3&1&1\end{matrix}\right|=-12$

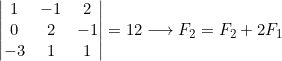
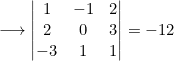
Si en un determinante se permutan dos de sus filas o columnas el valor del determinante cambia de signo.

Ejemplo

$\left|\begin{matrix}1&2&-2\\2&0&0\\-1&0&2\end{matrix}\right|=-8 \longrightarrow F_2\leftrightarrow F_1\longrightarrow \left|\begin{matrix}2&0&0\\1&2&-2\\-1&0&2\end{matrix}\right|=8$

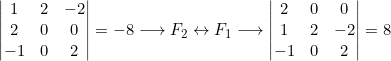
Si se multiplican todos los elementos de una fila o columna por un mismo número el valor del determinante también se multiplica por dicho número.

Ejemplo

$\left|\begin{matrix}3\cdot a&3\cdot b&3\cdot c\\d&e&f\\g&h&i\end{matrix}\right|=3\cdot \left|\begin{matrix}a&b&c\\d&e&f\\g&h&i\end{matrix}\right|$

$\left|\begin{matrix}a&b&2\cdot c\\d&e&2\cdot f\\g&h&2\cdot i\end{matrix}\right|=2\cdot \left|\begin{matrix}a&b&c\\d&e&f\\g&h&i\end{matrix}\right|$

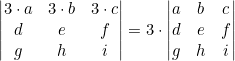
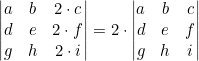
El determinante de una matriz cuadrada tiene el mismo valor que el de su traspuesta.

$\left|A\right|=\left|A^t\right|$

Ejemplo

$\left|\begin{matrix}1&2&-1\\2&0&-2\\3&0&-1\end{matrix}\right|=\left|\begin{matrix}1&2&3\\2&0&0\\-1&-2&-1\end{matrix}\right|$

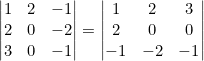
El determinante del producto de dos matrices es el producto de los determinantes de estas matrices por separado.

Ejemplo

$\left|\begin{pmatrix}1&1&0\\2&-1&1\\-2&0&1\end{pmatrix}\cdot\begin{pmatrix}2&1&-3\\2&1&5\\0&2&1\end{pmatrix}\right|=\left|\begin{matrix}1&1&0\\2&-1&1\\-2&0&1\end{matrix}\right|\cdot\left|\begin{matrix}2&1&-3\\2&1&5\\0&2&1\end{matrix}\right|$

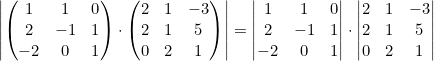
El determinante de una matriz triangular es el producto de los elementos de su diagonal principal.

Ejemplo

$\left|\begin{matrix}1&2&1&-3\\0&-2&2&1\\0&0&2&1\\0&0&0&-1\end{matrix}\right|=1\cdot(-2)\cdot2\cdot(-1)=4$

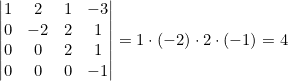
Cuando dos determinantes tienen todas sus filas o columnas iguales menos una, su suma es igual al valor del determinante que se forma al dejar las filas o columnas iguales igual y sumar los elementos de la fila o columna que es distinta.

Ejemplo

$\left|\begin{matrix}1&2&-1\\-1&1&0\\-1&0&4\end{matrix}\right|+\left|\begin{matrix}1&2&-1\\2&-1&-1\\-1&0&4\end{matrix}\right|=\left|\begin{matrix}1&2&-1\\1&0&-1\\-1&0&4\end{matrix}\right|$

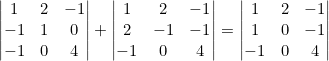
Tras ver esto podemos ver como estas propiedades de los determinantes son muy útiles para hallar rápidamente el valor de un determinante en lugar de desarrollarlo y más usos que veremos más adelante.

$\text{}$